Question

The coordinates of the vertices of a triangle are E(4,5), F(16,17 and G(10, 5) Let H be the midpoint of segment "EG" and let J be the midpoint of segment "FG".Verify the Triangle Midsegment Theorem by showing that segment "HJ" is parallel to segment "EF" and HJ = 1/2EF.

Answer 1

The coordinates of the vertices of a triangle are E(4,5), F(16,17 and G(10, 5) Let H be the midpoint of segment "EG" and let J be the midpoint of segment "FG".





Verify the Triangle Midsegment Theorem by showing that segment "HJ" is parallel to segment "EF" and HJ = 1/2EF.

step 1

Find out the midpoint H

The formula to calculate the midpoint between two points is equal to

`((x1+x2)/(2),(y1+y2)/(2))`

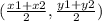
we have

E(4,5) and G(10, -5)

substitute given coordinates

`\begin{gathered} H=((4+10)/(2),(5-5)/(2)) \\ H(7,0) \end{gathered}`

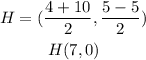
step 2

Find out the midpoint J

we have

F(16,17) and G(10, -5)

substitute

`\begin{gathered} J=((16+10)/(2),(17-5)/(2)) \\ J(13,6) \end{gathered}`

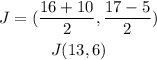
step 3

Find out the slope HJ

H(7,0) and J(13,6)

m=(6-0)/(13-7)

m=6/6

m=1

step 4

Find out the slope EF

we have

E(4,5), F(16,17)

m=(17-5)/(16-4)

m=12/12

m=1

step 5

Compare slope HJ and slope EF

their slopes are equal

that means

HJ and EF are parallel

step 6

Find out the distance HJ

the formula to calculate the distance between two points is equal to

`d=\sqrt[]{(y2-y1)^2+(x2-x1)^2}`

we have

H(7,0) and J(13,6)

substitute

`\begin{gathered} HJ=\sqrt[]{(6-0)^2+(13-7)^2} \\ HJ=\sqrt[]{(6)^2+(6)^2} \\ HJ=6\sqrt[]{2} \end{gathered}`

step 7

Find out the distance EF

we have

E(4,5), F(16,17)

substitute

`\begin{gathered} EF=\sqrt[]{(17-5)^2+(16-4)^2} \\ EF=\sqrt[]{(12)^2+(12)^2} \\ EF=12\sqrt[]{2} \end{gathered}`

step 8

Verify

HJ = 1/2EF

substitute

`\begin{gathered} 6\sqrt[]{2}=(1)/(2)\cdot(12\sqrt[]{2}) \\ 6\sqrt[]{2}=6\sqrt[]{2} \end{gathered}`

is true

that means

Triangle Midsegment Theorem was verified