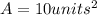Question

What is the area of a triangle where the vertices are (-3,-3), (-3,2), and (1,2)

Answer 1

Given:

The vertices of the triangle are (-3,-3), (-3,2), and (1,2).

Required:

We need to find the area of the given triangle.

Step-by-step explanation:

Mark the points on the graph and join them.

A(-3,2), B(-3,-3), and C(1,2).

The given triangle is a right-angled triangle.

The height of the given triangle is the length of AB.

The base length of the given triangle is the length of AC.

Consider the distance formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

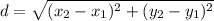
Use the distance formula to find the length of the line segments.

Consider the points A(-3,2) and B(-3,-3),

`Substitute\text{ }x_1=-3,y_1=2,x_2=-3\text{ and }y_2=-3\text{ in the formula.}`
`AB=√((-3-(-3))^2+(-3-2)^2)`
`AB=√((0)^2+(-5)^2)`
`AB=5units`

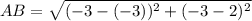
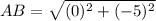
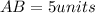
Consider the points A(-3,2) and C(1,2).

`Substitute\text{ }x_1=-3,y_1=2,x_2=1\text{ and }y_2=2\text{ in the formula.}`
`AC=√((1-(-3))^2+(2-2)^2)`
`AC=√((4)^2+(0)^2)`
`AC=4`

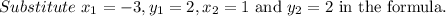
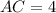
We get h=AB=5 and b=AC=4.

Consider the area of the triangle formula.

`A=(hb)/(2)`

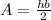
Substitute h=5 and b=4 in the formula.

`A=(5*4)/(2)`
`A=10units^2`

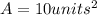
Final answer:

`A=10units^2`