We have to find the price of each pound of almonds and jelly beans.
We can call:
• A: price per pound of the almonds
,
• J: price per pound of the jelly beans
We know that 3 pounds of almonds and 8 pounds of jelly beans cost $23.
This means that the cost of the almonds, equal to quantity times price, and the cost of the jelly beans together is equal to $23.
We can write this as:
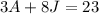
We also know that 5 pounds and 2 pounds of jelly beans cost $10. We can write this as:
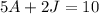
We can substract the first equation of 4 times the second equation and it will let us solve for A:
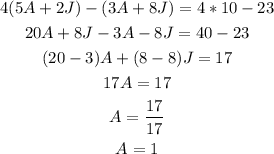
Knowing the price of the almonds (A = 1) we can use any of the original equations to find J:
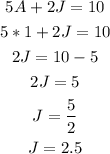
Answer:
Cost for each pound of almonds: $1
Cost for each pound of jelly beans: $2.50