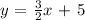1 Answer

PhABC · Answer 1 · 2023-02-11T20:44:00+0000

The equation of the line perpendicular to the given equation is;

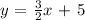
$y\text{ = }(3)/(2)x\text{ + 5}$

Option C is the correct answer

Here, we want to select which of the equations in the option is perpendicular to the given equation

Firstly, we need to understand that for two equations to be perpendicular, then the product of their slopes must be equal to -1

Before we proceed to compare, we need to write the equation in the general form

The equation of the line written in the general form will be;

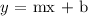
$y\text{ = mx + b}$

where m represents the slope and the term b represents the y-intercept

Now, let us proceed to write the equation in the standard form;

We have this as;

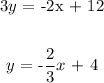
$\begin{gathered} 3y\text{ = -2x + 12} \\ \\ y\text{ = -}(2)/(3)x\text{ + 4} \end{gathered}$

Compared with the general form, we can see that the slope of this line is -2/3

Now let us get the slope of the line that would be perpendicular to it;

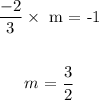
$\begin{gathered} (-2)/(3)*\text{ m = -1} \\ \\ m\text{ = }(3)/(2) \end{gathered}$

Now, the equation perpendicular to what was given will have a slope of 3/2

Fortunately, all the options in the question have been written in the general form

The one with a slope of 3/2 is option C

$y\text{ = }(3)/(2)x\text{ + 5}$

Please log in or register to add a comment.