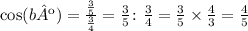ANSWER
cos(bº) = 4/5
Step-by-step explanation
When a triangle is dilated, the resulting triangle is similar to the original triangle. Therefore, the interior angles of the dilated triangle are congruent to the interior angles of the original triangle. This means that cos(bº) is the same for both triangles.
Using the relationship between these three trigonometric ratios:
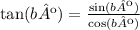
We can find the cosine: