For this problem we were given the distance to the moon and the width of a quarter in meters. We need to determine how many quarters we would need to stack in order to reach the moon.
In order to solve this problem, we need to divide the distance from the surface of the Earth to the moon by the width of each quarter. Notice that both numbers are presented in scientific notations, therefore we need to divide the coefficients and subtract the exponents. This is done below:
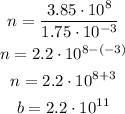
If Fin's claim were true, he'd need to stack a total of 2.2*10^11 quarters.