Given:
There are 11 letters in the word 'MISSISSIPPI'
The number of P's are 2.
The probability that the randomly chosen slip of paper have the letter P written on it is,
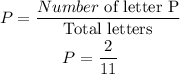
The probability that the randomly chosen slip of paperdoes not have the letter P written on it is,
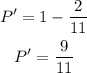
The odd against event is calculated as,
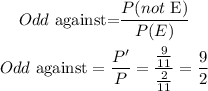
Answer: The odds against the paper having the letter P written on it is 9/2 (9:2)