Question

Given the general form: F( x )= a(x^2)+bx+cConvert it to vertex form (also known as standard form) by putting the values for a,h and k into the correct boxes.F(x)=a(x-h)^2+kIdentify the vertex(x,y)General form: F( x )=1 x^2+6 x +-1 Vertex form: F( x )= Answer for part 1 and coordinate 1 (x- Answer for part 1 and coordinate 2 )^2 +Answer for part 1 and coordinate 3Vertex: (Answer for part 2 and coordinate 1,Answer for part 2 and coordinate 2)

Answer 1

`\begin{gathered} Vertex\colon\: (-3,-10) \\ Vertex\: form\: equation\colon\: f(x)=(x+3)^2-10 \end{gathered}`

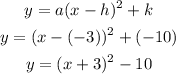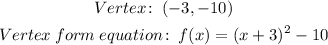
1) In order to convert from the standard version to the vertex form we'll need to find the vertex of that parabola:

`f(x)=x^2+6x-1`

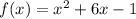
We can find the vertex, using these formulas:

`\begin{gathered} x=h=-(b)/(2a)=(-6)/(2)=-3 \\ k=(-3)^2+6(-3)-1=9-18-1=9-19=-10 \\ V(-3,-10) \end{gathered}`

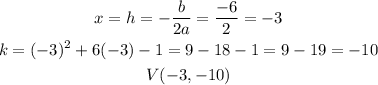
So this is the vertex of that parabola at point (-3,-10)

2) Now, note that the coefficient a = 1, and with the vertex, we can now rewrite that equation into the vertex form:

`\begin{gathered} y=a(x-h)^2+k \\ y=(x-(-3))^2+(-10) \\ y=(x+3)^2-10 \end{gathered}`