Question

O POLYNOMIAL AND RATIONAL FUNCTIONSFinding the maximum or minimum of a quadratic function

Answer 1

Given

The function,

`g(x)=x^2+4x`

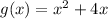
To find:

The maximum or minimum value of the function, and where does it occur.

Step-by-step explanation:

It is given that,

`g(x)=x^2+4x`

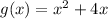
That implies,

Set g(x)=y.

Then,

`\begin{gathered} y=x^2+4x \\ y=(x+2)^2-4 \\ y+4=(x+2)^2 \end{gathered}`

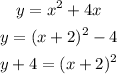
Here, a=1>0.

Then, the parabola opens up.

And, k is the minimum functional value, it occurs when x = h.

Therefore,

1) g(x) has a minimum value.

2) g(x)'s minimum value is -4.

3) And it occurs at x = -2.