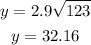we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
y=kx
where
k is the constant of proportionality
In this problem we have that
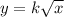
when y=29, x=100
step 1
find the value of k
substitute the given values in the expression above
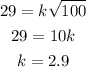
step 2
we have the equation
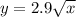
For x=123
substitute the value of x and solve for y