Question

Hello! Need some help on part c. The rubric, question, and formulas are linked. Thanks!

Answer 1

Step-by-step explanation:

The rate of increase yearly is

`\begin{gathered} r=69\% \\ r=(69)/(100)=0.69 \end{gathered}`

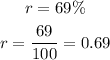
The number of lionfish in the first year is given beow as

`N_0=9000`

Part A:

To figure out the explicit formula of the number of fish after n years will be represented using the formula below

`P(n)=N_0(1+r)^n`

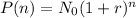
By substituting the formula, we will have

`\begin{gathered} P(n)=N_(0)(1+r)^(n) \\ P(n)=9000(1+0.69)^n \\ P(n)=9000(1.69)^n \end{gathered}`

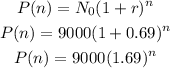
Hence,

The final answer is

`f(n)=9,000(1.69)^n`

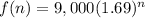
Part B:

to figure out the amoutn of lionfish after 6 years, we wwill substitute the value of n=6

`\begin{gathered} P(n)=9,000(1.69)^(n) \\ f(6)=9000(1.69)^6 \\ f(6)=209,683 \end{gathered}`

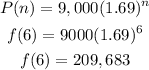
Hence,

The final answer is

`\Rightarrow209,683`

Part C:

To figure out the recursive equation of f(n), we will use the formula below

From the question the common difference is

`d=-1400`

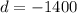
Hence,

The recursive formula will be

`f(n)=f_(n-1)-1400,f_0=9000`