Answer:
Volume of object = 42 cubic cm
Surface area of object = 96 square cm
Explanations:
The given figure is a triangular prism.The formula for calculating its volume is expressed as:
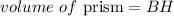
where:
B is the base area
H is the height of prism
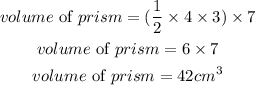
Determine the surface area of the prism
The surface area if the sum of all the faces of the prism.The faces consists of 3 rectangles and 2 triangles. The surface area is calculated as:
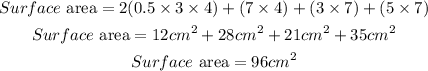
Hence the surface area of the object shown is 96 square cm