Given data:
* The radius of the turn is r = 40 m.
* The coefficient of friction is,
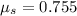
Solution:
The centripetal force acting on the car is,
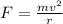
where m is the mass of the car,
The frictional force acting on the car is,
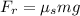
where g is the acceleration due to gravity,
In order to travel a car in rain, the centripetal force acting on the car must be equal to the frictional force on the same car.
Thus,
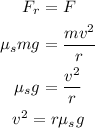
Substituting the known values,
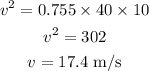
Thus, the maximum speed limit of the car in rain is 17.4 m/s.
Hence, the nearest possible correct answer is option b.