Question

Arc Length Formula:: Cx = degree measure of arcC-circumferenceDirections: Find each arc length. Round to the nearest hundredth.10. If EB = 15 cm, find the length of CD. 11. IF NR = 8 ft, find the length of NMP.DC12. IF VS = 12 m, find the length of UT.13. If JH = 21 in, fnd the length of KJG.12759DBS14. If FG = 27 yd, find the length of FED.15. If WS = 4.5 mm, find the length of TS.4780128317.62

Answer 1

Arc length formula:

`\begin{gathered} \text{Arc length=}(x)/(360)\cdot C \\ \\ C=2\pi r \\ r=\text{radius} \end{gathered}`

____________________________

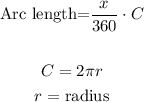
10. r= 15cm

Angle CED is supplementary with angle BEC (add up to 180°)

`\begin{gathered} m\angle\text{CED}+m\angle\text{BEC}=180 \\ \\ m\angle CED=180-m\angle BEC \\ m\angle CED=180-68 \\ m\angle CED=112 \end{gathered}`

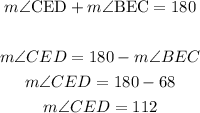
Then, arc CD is:

___________________________________________________

11. r=8ft

The measure of central angle MRQ is equal to the measure of the given arc MQ (162°) and this angle and angle NRP are vertical angles (have the same measure) then, angle MRN and QRP (also vertical angles) need to add up 360° with the other angles, use it to find the measure of angle MRN:

`\begin{gathered} m\angle NRP+m\angle NRP+m\angle MRN+m\angle QRP=360 \\ \\ 2m\angle NRP+2m\angle MRN=360 \\ 2(162)+2m\angle MRN=360 \\ 324+2m\angle MRN=360 \\ 2m\angle MRN=360-324 \\ m\angle MRN=(36)/(2) \\ \\ m\angle MRN=18 \end{gathered}`

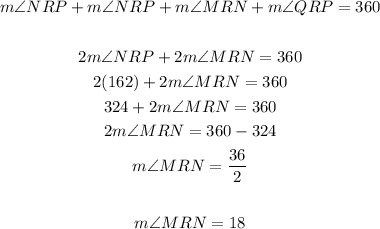
The angle for arc NMP is equal to the sum of angle MRP (180°) and angle MRN (18°).

Then, the length of arc NMP is:

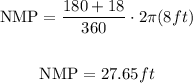
`\begin{gathered} \text{NMP}=(180+18)/(360)\cdot2\pi(8ft) \\ \\ \text{NMP}=27.65ft \end{gathered}`

___________________________