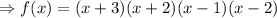Question

Please see the picture below,PART BUse the real zeros to factor f

Answer 1

Step-by-step explanation:

The polynomial is given below as

`f(x)=x^4+2x^3-7x^2-8x+12`

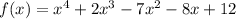
Given in the question above the real zeros are gotten below as

`x=-3,-2,1,2`

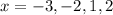
Concept:

To figure out the factor form of the polynoimial, we will equate each zero to x below as

`\begin{gathered} x=c \\ (x-c) \end{gathered}`

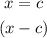
Therefore,

The factored form of the polynomial will be

`\begin{gathered} f(x)=x^(4)+2x^(3)-7x^(2)-8x+12 \\ x=-3,x=-2,x=1,x=2 \\ f(x)=(x+3)(x+2)(x-1)(x-2) \end{gathered}`

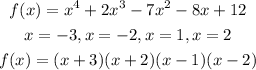
Hence,

Using the real zeros of f(x) , the factored form of the polynomial is

`\Rightarrow f(x)=(x+3)(x+2)(x-1)(x-2)`