Question

= 186x – 30y5х – 25y= 15

Answer 1

There are infinitely many solutions

Step-by-step explanation:

Given the system of linear equations:

`\mleft\{\begin{aligned}6x-30y=18 \\ 5x+25y=15\end{aligned}\mright.`

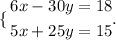
To solve using Matrices, we write the equation in the form:

Ax = b

Where A represent the matrix of the coefficient of the variables x and y

x represent the matrix of the variables x and y

and b represents the matrix of the constants on the right hand side.

In matrix form, we have:

`\begin{bmatrix}{6} & {-30} \\ {5} & {-25}\end{bmatrix}\begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{18} \\ {15}\end{bmatrix}`

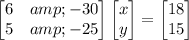
We must have a nonzero determinant for A

The determinant of A is:

`\begin{gathered} (-25*6)-(-30*5) \\ =-150+150 \\ =0 \end{gathered}`

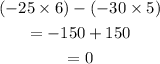
The determinant of A is zero, without going far, we conclude that the system has infinite number of solutions.