The tangent-secant theorem states that given the segments of a secant segment and a tangent segment that share an endpoint outside of the circle, the product of the lengths of the secant segment and its external segment equals the square of the length of the tangent segment.
Graphically,
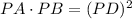
In this case, we have:
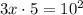
Now, we can solve the equation for x:
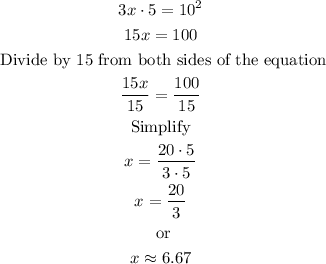
Therefore, the value of x is 20/3 or approximately 6.67.