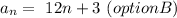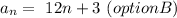
Step-by-step explanation:
For an arithmetric progression, we need to find the common difference in the sequence
common difference = d = 2nd term - 1st term = 3rd term - 2nd term = 4th term - 3rd term
2nd term - 1st term = 27 -15 = 12
3rd term - 2nd term = 39-27 = 12
The result are the same.
Hence, d = 12
The first trm = 15
The formula for arithmetric sequence:
The nth term = 1st term + d(n - 1)
Replacing with the values we got above:
The nth term = 15 + 12(n - 1)
Since none of the options have the above, we would expand the parenthesis.
The nth term = 15 + 12×n - 12×1
The nth term = 15 + 12n - 12
= 15 -12 + 12n
The nth term = 3 + 12n = 12n + 3
From the options:
The nth term = 12n + 3 (option B)