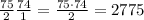To calculate the combinations of groups of 2, since the order doesn't matter, we can use combination. In this case we have a total of 75 to choose from and will choose 2, so this is "75 choose 2".
The equation to use is (n choose k):
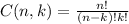
In this case, we have n = 75 and k = 2, so:
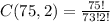
For the property of factorials, 75! / 73! = 75*74, because the terms less or equal 73 cancel out. so:
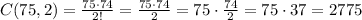
So, there are 2775 different groups of 2 in this case.
Another way of doing this calculation is by thinking of choosing one at a time.
At first, we can choose from 75 possible people, so we start at 75.
When we choose the second one, we already picked the first, so there are only 74 people left. So we get:

This are the two first people, but, in this way we are considering too many groups, since here we considere the order matter, to fix this we divide by k!, where k is the number of picks, which is 2 in this case (so, permutation of 2). So: