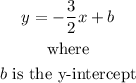Part 2:
To determine an equation that is perpendicular to the line equation y = -3/2x + 12, get the negative reciprocal of the slope of the line equation.

Part 3:
An equation that is parallel to the line y = -3/2x + 12, is a line equation that will have the same slope as the original line.
Given that the slope of the line is m = -3/2, then any line equation in the form