Question

Determine the orderd pair (8,-3)is a solytion to the linear pair

Answer 1

To answer this question, we need to evaluate if the ordered pair forms an identity with both equations. We need to substitute the values for x = 8, and y = -3 in both equations:

`(x)/(2)+5y=-11\Rightarrow(8)/(2)+5(-3)=-11\Rightarrow4-15=-11\Rightarrow-11=-11`

These values result in an equality in this equation. We need to evaluate the other equation:

`6x-(y)/(6)=40\Rightarrow6\cdot(8)-((-3)/(6))=40\Rightarrow48+(1)/(2)=(97)/(2)\\e-11`

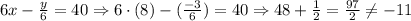
In this case, the values do not result in an equality in one of both equations.

Therefore, we have that the correct answer is the option B:

No, the proposed solution does not result in an equality in one of the two equations.