We will have the following:
a) We first determine the time it takes to travel the distance to both vehicles:
*
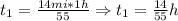
*
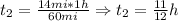
So, we determine now the difference in time:
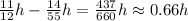
So, the fastest car will arrive approximately 0.66 hours sooner.
b) We determmine the distance it must travel the fastest car to have a 15 minute lead on the other one as follows:
First, we determine the time difference required:
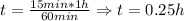
Then, since both vehicles will move relative to each other, we will have that:
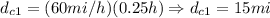
So, the fastest car must be 15 miles ahead of the other car in order to have a 15 minute lead with respect to the second car.