Question

Determine the value of k for which f(x) is continuous.

Answer 1

These are the conditions of the continuity in a function:

First, the value of x must have an image.

Second, the lateral limits must be equal:

`\lim_(x\to a^+)f(x)=\lim_(x\to a^-)f(x)`

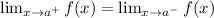
Finally, the value of the limit must be equal to the image of x. This means that:

`f(a)=\lim_(x\to a^)f(x)`

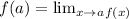
In this case, we must find a value of k that can make the two lateral limits equal in x =3:

`\lim_(x\to3^+)x^2+k=\lim_(x\to3^-)kx+5`

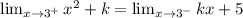
We can solve these two limits easily by replacing the x with the value of 3

`3^2+k=3k+5`
`\begin{gathered} 9+k=3k+5 \\ 4=2k \\ k=2 \end{gathered}`

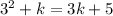
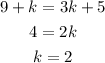
Finally, we can see that the answer is k=2.