Question

Molly was on a long 136 mile road trip. The first part of the trip there was lots of traffic, she only averaged 16 mph. The second part of the trip there was no traffic so she could drive 44 mph. If the trip took her 5 hours, how long did she travel at each speed? In traffic she drove for _____ hours After the traffic cleared she drove for ____ hours.

Answer 1

In traffic, she drove for 3 hours

and After the traffic cleared she drove for 2 hours.

Step-by-step explanation:

Given that the road trip was 136 miles;

`d=136`

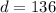
The first part of the trip there was lots of traffic, she only averaged 16 mph;

`v_1=16`

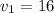
The second part of the trip there was no traffic so she could drive 44 mph;

`v_2=44`

She traveled for a total of 5 hours;

`t=5`

let x represent the time in traffic when she traveled at 16 mph

`t_1=x`

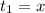
the time the traffic is clear would be;

`t_2=t-t_1=5-x`

Recall that distance equals speed multiply by time;

`d=v_1t_1_{}_{}^{}+v_2t_2`

substituting the values;

`136=16x+44(5-x)`

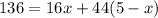
solving for x;

`\begin{gathered} 136=16x+220-44x \\ 44x-16x=220-136 \\ 28x=84 \\ x=(84)/(28) \\ x=3 \end{gathered}`

So;

`\begin{gathered} t_1=3\text{ hours} \\ t_2=5-x=5-3=2 \\ t_2=2\text{ hours} \end{gathered}`

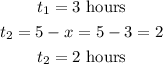
Therefore, In traffic, she drove for 3 hours

and After the traffic cleared she drove for 2 hours.