Answer
x = 1 or x = n.a.
Explanation
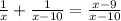
Multiplying by (x - 10) at both sides of the equation:
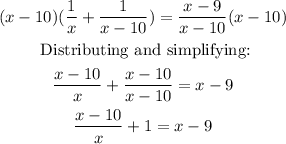
Multiplying by x at both sides of the equation:

Subtracting 2x and adding 10 at both sides of the equation:
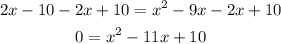
We can solve this equation with the help of the quadratic formula with the coefficients a = 1, b = -11, and c = 10, as follows:
![\begin{gathered} x_(1,2)=\frac{-b\pm{}√(b^2-4ac)}{2a} \\ x_(1,2)=\frac{11\pm\sqrt{(-11)^2-4\cdot1\operatorname{\cdot}10}}{2\operatorname{\cdot}1} \\ x_(1,2)=(11\pm√(81))/(2) \\ x_1=(11+9)/(2)=10 \\ x_2=(11-9)/(2)=1 \end{gathered}]()
The solution x = 10 is not possible because it makes zero the denominator in 2 of the rational expressions of the original equation. In consequence, it must be discarded.