The equation of a line in Slope-Intercept form, is:

Where "m" is the slope of the line and "b" is the y-intercept.
By definition:
- The slopes of parallel lines are equal and the y-intercepts are different.
- The slopes of perpendicular lines are opposite reciprocals.
For this case you need to rewrite the equations given in the exercise in Slope-Intercept form by solving for "y".
- Line #1:
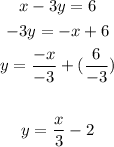
You can identify that:
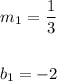
- Line #2:
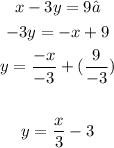
You can identify that:
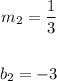
Therefore, since:
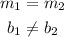
You can conclude that: The graphs of the equation are parallel.