y=-5x-26
Step-by-step explanationthe equation of a line can be written as:
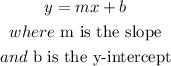
now, when we have the slope and a passing point, we need to use the slope-point formula , it says
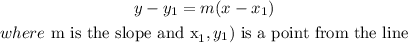
so
Step 1
a)let
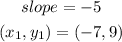
b) now replace in the slope-point formula and solve for y
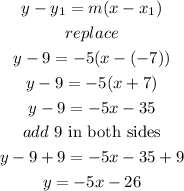
therefore, the equaton of the line is
y=-5x-26
I hope this helps you