Question

Determine the corresponding general form of each of the following vertex form

1. y = (x– 1)2

A. y = x2+ x + 1
B. y = x2 – 2x – 1
C. y = x2 – 2x + 1

2. y = (x + 4)2– 5

A. y = x2+ 8x – 11
B. y = x2+ 8x – 21
C. y = x2+ 8x + 21

3. y = -(x + 9)2– 10

A. y = -x2– 18x + 91
B. y = -x2– 18x – 91
C. y = -x2– 18x – 71

4. y = 3(x + 2)2– 18

A. y = 3x2+ 12x – 6
B. y = 3x2+ 12x + 6
C. y = 3x2+ 12x – 14

5. y = -2(x + 1)2– 16

A. y = -2x2– 4x – 18
B. y = -2x2– 4x – 2
C. y = -2x2– 4x – 14

6. y = 5(x + 5)2

A. y = 5x2+ 50x + 125
B. y = 5x2+ 50x + 25
C. y = 5x2+ 25x + 125

7. y =1/2(x + 8)2– 8

A. y = 1/2x2 + 8x + 24
B. y= 1/2x + 8x – 40
C. y = 1/2x2 + 16x + 24

8. y = (x + 3/2)2 + 3/4

A. y = x2+ 3x + 2
B. y = x2 + 6/4x + 12/16
C. y = x2 + 3x + 3

9. y = 2(x + 8)2– 5x

A. y = 2x2 + 32x + 59
B. y = 2x2 + 27x + 128
C. y = 2x2+ 37x + 64

10. y = -5(x – 4)2+ 15
A. y = -5x2+ 40x – 65
B. y = -5x2 – 40x – 65
C. y = -5x2+ 40x + 65​​

Answer 1

Explanation:

(a + b)² =a² + 2ab + b²

(a -b)² = a² - 2ab + b²

1) y = (x -1)²

y= x² - 2*x*1 + 1

y = x² - 2x + 1

Ans: C

2)y = (x +4)² + 5

y = x² +2*x*4 + 4² + 5

= x² + 8x + 16 + 5

y = x² + 8x + 21

C

3) y = -(x + 9)²- 10

y = - [x² + 18x + 81] - 10

= -x² - 18x - 81 - 10

y =-x² - 18x - 91

B

4) y = 3(x + 2)² - 18

y =3 [x² + 4x + 4] - 18

y = 3x² + 12x + 12 - 18

y =3x² + 12x - 6

A

5) y = -2(x + 1)² - 16

= -2[x² + 2x + 1] -16

= -2x² - 4x - 2 - 16

y = -2x² - 4x - 18

A

6) y = 5(x + 5)²

=5[x²+ 10x + 25]

y = 5x² +50x + 125

A

7)y = (1/2)(x + 8)² - 8

y = (1/2) (x² + 16x + 64) - 8

`y = (1)/(2)*x^(2)+ (1)/(2)*16x + (1)/(2)*64 -8\\\\\\y =(1)/(2)x^(2)+8x +32 - 8\\\\\\y=(1)/(2)x^(2) +8x + 24`

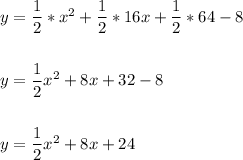
A

8) y = (x + 3/2)² + 3/4

`y = x^(2) +2*x*(3)/(2)+(9)/(4)+(3)/(4)\\\\y=x^(2)+3x+(12)/(4)\\\\\\y=x^(2)+3x + 3`

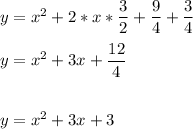
C

9) y = 2[x² + 16x + 64] - 5x

y = 2x² + 32x + 64 - 5x

y =2x² + 27x + 6