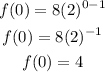Question

From the given information. Write the recursive and explicit functions for each geometric sequence. Please use these terms. recursive f(1) = first term, f(n) = pattern*f(n-1). what is the 1st term and pattern? explicit is y = pattern^x * 0 term. work backwards to find 0 term

Answer 1

We know that a geometric sequence is given by:

`f(n)=f(1)r^(n-1)`

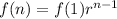
where r is the common ratio of the sequence.

For this sequence we have that the common ratio is r=2, this comes from the fact that in the first day we have 6 dots, for the second day we have twelve and for the third day we have 24. We also notice that the first term is:

`f(1)=8`

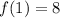
Therefore the sequence is given by:

`f(n)=8(2)^(n-1)`

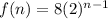
Now, to find the zeoth term we plug n=0 in the sequence above, therefore the zeroth term is:

`\begin{gathered} f(0)=8(2)^(0-1) \\ f(0)=8(2)^(-1) \\ f(0)=4 \end{gathered}`