Question

The cost C (in dollars) of producing x units of a product is given by the following. C= 2.6. Square root of x + 600

Answer 1

The marginal cost in dollars of producing x units is given by the next equation:

`C=2.6\sqrt[]{x}+600`

a)

To find the marginal cost (in dollars per unit) when x= 9.

Then, we need to replace x=9 on the derivation of the cost equation:

So:

`(d)/(dx)C=\frac{1.3}{\sqrt[]{x}}`

Where:

`(d)/(dx)2.6\sqrt[]{x}=2.6(d)/(dx)\sqrt[]{x}=2.6(d)/(dx)^{}x^{(1)/(2)}=2.6\cdot(1)/(2)x^{(1)/(2)-1}=1.3\cdot x^{-(1)/(2)}=\frac{1.3}{\sqrt[]{3}}`

and, the derivate of a constant is equal to zero.

`(d)/(dx)600=0`

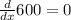
Replacing x= 9

`(d)/(dx)C=\frac{1.3}{\sqrt[]{9}}`

Hence, the marginal cost is equal to:

`(d)/(dx)C=0.43`

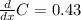
b) Now, when the production increases 9 to 10. It's the same as the cost of producing one more machine beyond 9.

Then, it would be x=10 on the cost equation:

`C=2.6\sqrt[]{x}+600`
`C=2.6\sqrt[]{10}+600`
`C=608.22`

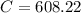
and x= 9

`C=2.6\sqrt[]{9}+600`
`C=2.6(3)+600`
`C=607.8`

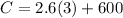
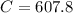
Then, we calculate C(10) - C(9) =

`608.22-607.8`
`=0.43`

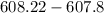
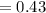
C)

Both results are equal.

Hence, the marginal cost when x=9 is equal to the additional cost when the production increases from 9 to 10.