We are going to solve the question using the quadratic formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{(b^2}-4ac)}{2a} \\ \text{where the quadratic equation is ax}^2+bx+c=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vpla0mx0pjb3xk6aoppa6jlcs6q2ud184g.png)
The quadratic equation given is
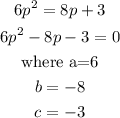
By substitution we will have,
![\begin{gathered} p=\frac{-(-8)\pm\sqrt[]{(-8)^2}-(4*6*-3)}{2*6} \\ p=\frac{8\pm\sqrt[]{64+72}}{12} \\ p=\frac{8\pm\sqrt[]{136}}{12} \\ p=\frac{8\pm\sqrt[]{4*34}}{12} \\ p=\frac{8\pm2\sqrt[]{34}}{12} \\ p=\frac{2(4\pm\sqrt[]{34)}}{12} \\ p=\frac{4\pm\sqrt[]{34}}{6} \\ p=\frac{4+\sqrt[]{34}}{6}\text{ or p=}\frac{4-\sqrt[]{34}}{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m9j33kcnz2mrwc0edwhuoh54jfydchnpoz.png)
Therefore,
With the roots gotten from the quadratic equation, we can therefore deduce that the solutions to the equation 6p²=8p+3 will give 2 irrational roots.
The correct answer is OPTION D