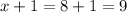Answer:
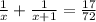
The two consecutive positive integers are 8 and 9.
Step-by-step explanation:
Let the 1st positive integer be x and the 2nd be x + 1, so their reciprocal will be 1/x and 1/x+1.
The equation can then be written as;
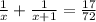
To solve for x, the 1st step is to find the LCM of the left-hand side of the equation;
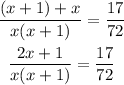
We can equate the numerators and solve for x as shown below;
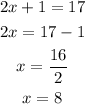
If the 1st positive integer, x, is 8, therefore the 2nd integer, x + 1, will be;