Question

What are all the factors of 54?

Answer 1

Explanation:

1 × 54 = 54, (1, 54) is a pair factor of 54.

2 × 27 = 54, (2, 27) is a pair factor of 54

3 × 18 = 54, (3, 18) is a pair factor of 54

6 × 9 = 54, (6, 9) is a pair factor of 54

Therefore, the positive pair factors are (1, 54), (2, 27),(3, 18) and (6, 9).

Answer 2

To find the factors of a number, we can look for factors to divide it by subsequently.

It is easier to start with lower factors.

Let's start by "2".

Since "54" is even, it is divisable by "2":

`(54)/(2)=27`

So "2" is one of the factors.

Now, we have got 27. It is not even anymore, but it is divisable by "3":

`(27)/(3)=9`

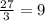
So "3" is another factor.

Now we have got "9" and it is also divisable by "3":

`(9)/(3)=3`

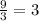
So there is another "3" factor.

And since we have got now another "3", we know it is divisable by "3":

`(3)/(3)=1`

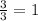
Now we have got to "1", so we found all the prime factors:

`54=2\cdot3\cdot3\cdot3`

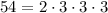
Now,, we need to combine them to find all possible combinations.

We will start from low to high.

"1" is always a factor.

There is "2" there, so it is also a factor.

Then we have "3" as another factor.

There is no need to combine "1" with another factor, so we will start b combining 2 and 3:

`2\cdot3=6`

So, "6" is another factor.

We can combine 3 with 3:

`3\cdot3=9`

"9" is another factor.

Now we start combining three of them:

`\begin{gathered} 2\cdot3\cdot3=6\cdot3=18 \\ 3\cdot3\cdot3=9\cdot3=27 \end{gathered}`

So, "18" and "27" are factors.

And now we combine 4 of them, but this is get us back to "54" which is the last factor.

So, the factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54.