Answer:
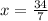
Explanations:
Given the function defined as:
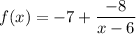
The function can further be expressed as:
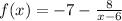
Find the LCM of the function;
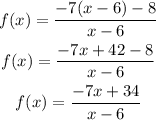
If f(x) = 0, then the value of x is calculated as:
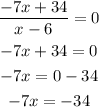
Divide both sides of the equation by -7:
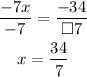
Therefore the value of x if f(x) = 0 is 34/7