Question

Given that tank=8 and sinx is negative determine sin(2x) cos(2x) and tan(2x)

Answer 1

sin2x = 16/65

cos2x = -63/65

tan2x = -16/63

Step-by-step explanation:

the tangent of an angle is equal to the opposite side over the adjacent side. So, if the tan(x) = 8, we can represent this as the following diagram:

Therefore, we can calculate the value of the hypotenuse as:

`\text{Hypotenuse = }\sqrt[]{8^2+1^2}=\sqrt[]{64+1}=\sqrt[]{65}`

With the hypotenuse, we can calculate sin(x) and cos(x) as follows:

`\begin{gathered} \sin x=(Opposite)/(hypotenuse)=-\frac{8}{\sqrt[]{65}} \\ \cos x=\frac{\text{Adjacent}}{\text{hypotenuse}}=-\frac{1}{\sqrt[]{65}} \end{gathered}`

We type the negative sign because the question says that sin(x) is negative.

Now, we will use the following trigonometric identities to find sin(2x), cos(2x) and tan(2x)

`\begin{gathered} \sin 2x=2\sin x\cos x \\ \cos 2x=1-2\sin ^2x \\ \tan 2x=(2\tan x)/(1-\tan ^2x) \end{gathered}`

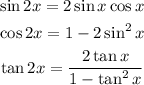
Therefore, replacing the values, we get:

`\sin 2x=2(\frac{-8}{\sqrt[]{65}})(\frac{-1}{\sqrt[]{65}})=(16)/(65)`
`\cos 2x=1-2(\frac{-8}{\sqrt[]{65}})^2=1-2((64)/(65))=-(63)/(65)`
`\tan 2x=(2(8))/(1-8^2)=-(16)/(63)`

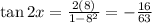
So, the answers are:

sin2x = 16/65

cos2x = -63/65

tan2x = -16/63