Question

There are two machines that produce aluminum cans. The newer machine can produce 5700 cans in 190 minutes. It takesthe older machine 285 minutes to produce that many cans. If the two machines work together, how long will it take them to produce 5700 cans?

Answer 1

114 minutes

Step-by-step explanation

Step 1

find the rate of production of each machine (cans per minute)

so

a)The newer machine:

`\begin{gathered} rate=\frac{cans\text{ }}{time} \\ rate_1=\frac{5700\text{ cans}}{190\text{ minutes}}=30\text{ }(cans)/(minute) \end{gathered}`

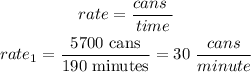
b)the older machine:

`\begin{gathered} rate=\frac{cans\text{ }}{time} \\ rate_2=\frac{5700\text{ cans}}{285\text{ minutes}}=20\text{ }(cans)/(minute) \end{gathered}`

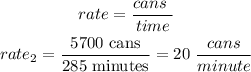
Step 2

Add the rates together to determine their combined

`\begin{gathered} rate_(total)=rate_1+rate_2 \\ rate_(total)=30\text{ }(cans)/(minute)+20(cans)/(m\imaginaryI nute) \\ rate_(total)=50\text{ }(cans)/(minute) \end{gathered}`

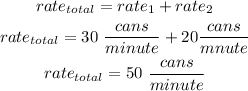
so, the total rate( both machine working ) is 50 cans per minute

Step 3

finally, to find the time to produce 5700 cans, divide the total cans by the rate, so

`\begin{gathered} time=\frac{number\text{ of cans}}{rate} \\ time=\frac{5700\text{ cans}}{50(cans)/(minute)}=114minutes \\ time=\text{ 114 minutes} \end{gathered}`

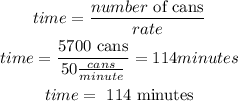
therefore, the answer is 114 minutes

I hope this helps you