Answer:
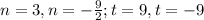
Explanation:
Second one is faster, so let's get rid of it first.
Divide by 2 to make numbers easier, and we get
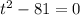 . You should recognize 81 is 9 squared, and both
. You should recognize 81 is 9 squared, and both
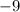 and
and
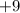 , when squared, give 81, we have our solution.
, when squared, give 81, we have our solution.
Now the first. I can't spot any quick trick to solve it, so quadratic formula it is. Let's rememer it: if
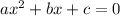 then
then
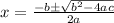
Let's bring the first equation in the standard form and calculate the quantity over the square root (usually called with the greek letter delta,
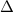 ) to the side.
) to the side.
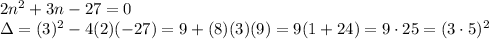
now we can apply the formula:
 Let's split the two cases now
Let's split the two cases now
