We have a direct proportionality between y and x.
If "k" is the constant of proportionality, the equation for this situation is:
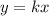
To find the constant of proportionality, we solve that equation for k:
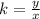
And since when y=45, x=180, substituting these values to find k:
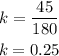
Now, we substitute the value of k into the equation of proportionality:
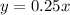
And in this equation, we can substitute any value of the variables, and find the value of the other variable.
In this case, we have y=90, so we substitute that value and solve for x:
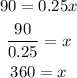
Answer: when y=90, x=360