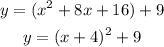Question

Express the equation y=x^2+8x+25 in the form y=a(x-h)^2+ka. y=a(x-h)^2+kb. y=(x+4)^2+9c. y=(x-4)^2-9d.y=(x-4)^2+9

Answer 1

The answer is B. y = (x + 4)^2 + 9

EXPLANATION :

From the problem, we have :

`y=x^2+8x+25`

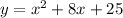
Group the terms in which the constant term and the terms with variables are separated.

`y=(x^2+8x)+(25)`

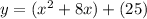
add and subtract a variable m to the parenthesis to maintain equivalency.

`y=(x^2+8x+m)+(25-m)`

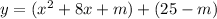
Calculate the value of m using b^2/4a^2 with a = 1 and b = 8

`m=(b^2)/(4a^2)=(8^2)/(4(1^2))=16`

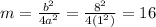
Then :

`\begin{gathered} y=(x^2+8x+16)+(25-16) \\ y=(x^2+8x+16)+(9) \end{gathered}`

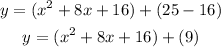
The first parenthesis will be a perfect square trinomial.

Factor and simplify :

`\begin{gathered} y=(x^2+8x+16)+9 \\ y=(x+4)^2+9 \end{gathered}`