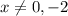Question

Find all values for which at least one denominator is equal to 0.

Answer 1

Given:

There are given the expression:

`(4)/(x+2)-(5)/(x)=1`

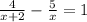
Step-by-step explanation:

To find the value of x that is equal to 0, we need to perform LCM in the denominator and then find the value for x:

Then,

From the given expression:

`\begin{gathered} (4)/(x+2)-(5)/(x)=1 \\ (4x-5(x+2))/(x(x+2))=1 \end{gathered}`

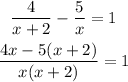
Then,

According to the question, the values at least one denominator is equal to .

So,

`\begin{gathered} x(x+2)=0 \\ x=0 \\ x+2=0 \\ x=-2 \end{gathered}`

Final answer:

Hence, the value of x is shown below:

`x\\e0,-2`