SOLUTION
We will be using the annual compound interest formula to solve this question.
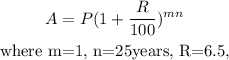
After a down payment of 0.15 x $225,000 = $33750
The principal value will be $225,000 - $33750 = $191250
Put all these values into the compound interest formula above,
we will have:
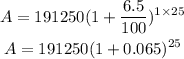
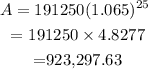
The mortgage total if they finance the closing costs will be:
$923,297.63