To draw a triangle, you cannot take three random line segments, they have to satisfy the triangle inequality theorems.
0. Triangle Inequality Theorem One: the lengths of any two sides of a triangle must add up to more than the length of the third side.
Procedure:
• Evaluating the first values given: (adding the two smallest values)
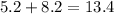
Now, we have to compare this addition with the bigger value. As 13.4 > 12.8, these can be side lengths of a triangle.
• Evaluating the second values given: (adding the two smallest values)
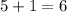
Comparing this addition with the bigger value, we can see that 6 < 10, meaning that these values cannot be side lengths of a triangle.
• Evaluating the third values given: (adding the two smallest values)
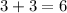
Comparing, we can see that 6 < 15. Therefore, these cannot be side lengths of a triangle.
• Evaluating the final values given:
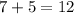
We can see that 12 < 13, so these cannot be side lengths of a triangle.
Answer:
• 12.8, 5.2, 8.2: ,can be side lengths of a triangle.
,
• 5, 10, 1: ,cannot be side lengths of a triangle.
,
• 3, 3, 15: ,cannot be side lengths of a triangle.
,
• 7, 13, 5: ,cannot be side lengths of a triangle.