Answer:
The pair one functions are given below as
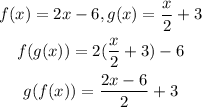
Step 1:
From pair 1, substitute the value of x=1 in the
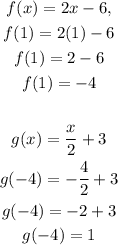
Step 2:
For pair 2, substitute x=1
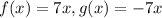
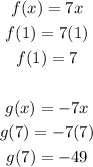
Step 3:
From pair one,
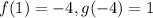
From pair 2,
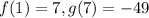
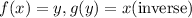
From the above conclusion, we can say that
The final answer is
PAIR 1 ONLY
OPTION B is the right answer