Question

Hello.
How to prove that those operations are truth?
Sums

Answer 1

a. This is just shifting the index of summation:

`\displaystyle \sum_(j=0)^4 d_(j+1) = d_(0+1)+d_(1+1)+\cdots+d_(4+1) \\ = d_(2-1)+d_(3-1)+\cdots+d_(6-1) \\ = \sum_(j=2)^6 d_(j-1)`

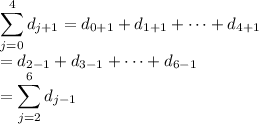
and just swap j with k, since you can freely use any symbol for the index.

That is, the identity relies on simple integer arithmetic: 0 + 1 = 1 = 2 - 1, and 1 + 1 = 2 = 3 - 1, and so on.

b. This is something of a generalization of the identity in part a.

`\displaystyle \sum_(j=1)^n a_jb_(m+j) = a_1b_(m+1) + a_2b_(m+2) + \cdots + a_nb_(m+n) \\ = a_((m+1)-m)b_(m+1) + a_((m+2)-m)b_(m+2) + \cdots + a_((m+n)-m)b_(m+n) \\ = \sum_(j=m+1)^(m+n) a_(j-m)b_j`

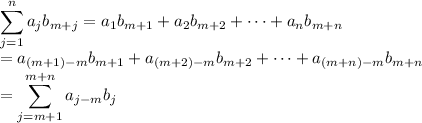
c. Distribute the summation to get

`\displaystyle \sum_(j=1)^m (6d_j+1) = \sum_(j=1)^m 6d_j + \sum_(j=1)^m 1`

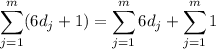
The second sum here is just adding together m copies of 1,

`\displaystyle \sum_(j=1)^m 1 = \underbrace{1+1+\cdots+1}_(m\,\rm times) = m`

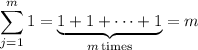
so

`\displaystyle \sum_(j=1)^m (6d_j+1) = \sum_(j=1)^m 6d_j + m`

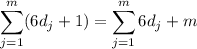
d. The sum as given is generally not true:

`\displaystyle \sum_(n=1)^k a_k = a_1+a_2+\cdots+a_k`

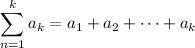
while (generalizing the identity from part c)

`\displaystyle \sum_(m=2)^(k+1) (a_m-1) = (a_2+a_3+\cdots+a_k+a_(k+1))-k`

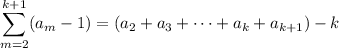
and these expressions are equal only if
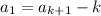`a_1=a_(k+1)-k`.