Question

A 228-turn, 24.506-cm-diameter coil is at rest in a horizontal plane. A uniform magnetic field 27 degrees away from vertical increases from 0.807 T to 4.68 T in 13.843 s. Determine the emf induced in the coil.

Answer 1

Given:

• Number of turns, N = 228

,

• Diameter, d = 24.506 cm

,

• θ = 27 degrees

,

• Initial Magnetic field, B1 = 0.807 T

,

• Final, B2 = 4.68 T

,

• Time , t = 13.843 s

Let's find the induced emf in the coil.

To find the induced EMF, apply Faraday's law:

`\begin{gathered} E=N(d)/(dt)(B*A) \\ \\ E=N*Acos\theta(d)/(dt)(B) \\ \\ E=N*(\pi r^2)cos\theta((B_2-B_1)/(t)) \end{gathered}`

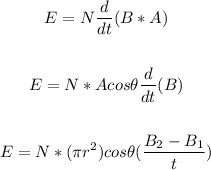
Where:

A is the area in meters.

Rewrite the diameter from cm to meters.

Where:

100 cm = 1 meters

24.056 cm = 0.24506 m

Now, the radius will be:

radius = diameter/2 = 0.24506/2 = 0.12253 m

Now, plug in the values and solve for E:

`\begin{gathered} E=228*(\pi *(0.12253)^2)cos(27)*((4.68-0.807)/(13.843)) \\ \\ E=228*0.0471666*cos(27)*0.27978 \\ \\ E=2.6\text{ volts} \end{gathered}`

Therefore, the EMF induced in the coil is 2.6 volts.

ANSWER:

2.6 v