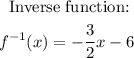Question 14.
Given the function:
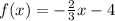
Let's find the inverse of the function.
To find the inverse, take the following steps.
Step 1.
Rewrite f(x) for y
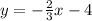
Step 2.
Interchange the variables:
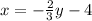
Step 3.
Solve for y
Add 4 to both sides:
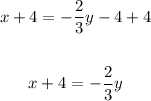
Multply all terms by 3:
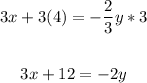
Divide all terms by -2:
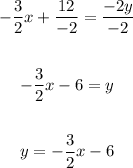
Therefore, the inverse of the function is:
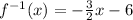
Let's graph both functions.
To graph each function let's use two points for each.
• Main function:
Find two point usnig the function.
When x = 3:
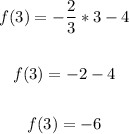
When x = 0:
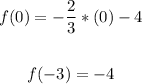
For the main function, we have the points:
(3, -6) and (0, -4)
Inverse function:
When x = 2:
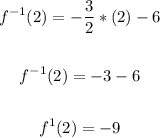
When x = -2:
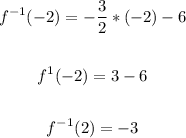
For the inverse function, we have the points:
(2, -9) and (-2, -3)
To graph both functions, we have:
ANSWER: