1 Answer

Ask a Question

Max Song · Answer 1 · 2023-03-28T02:09:31+0000

Sample

Mean

The formula to find the mean of a data set is:

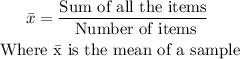
$\begin{gathered} \bar{x}=\frac{\text{Sum of all the items}}{\text{ Number of items}} \\ \text{ Where }\bar{\text{x}}\text{ is the mean of a sample} \end{gathered}$

So, in this case, we have:

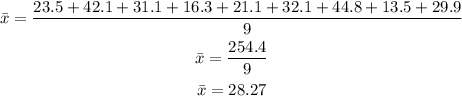
$\begin{gathered} \bar{x}=(23.5+42.1+31.1+16.3+21.1+32.1+44.8+13.5+29.9)/(9) \\ \bar{x}=(254.4)/(9) \\ \bar{x}=28.27 \end{gathered}$

Therefore, the mean of the given data set rounded to two decimal places is 28.27.

Standard deviation

The sample standard deviation formula is:

$\begin{gathered} s=\sqrt[]{\frac{\sum ^n_(i\mathop=1)(x_i-\bar{x})^2}{n-1}} \\ \text{ Where} \\ \text{ n is the number of data points} \\ x_i\text{ is each of the values of the data} \\ \bar{x}\text{ is the mean of the data set} \end{gathered}$

So, in this case, we have:

$\begin{gathered} s=\sqrt[]{((23.5-28.27)^2+(42.1-28.27)^2+(31.1-28.27)^2+(16.13-28.27)^2+(21.1-28.27)^2+(32.1-28.27)^2+(44.8-28.27)^2+(13.5-28.27)^2+(29.9-28.27)^2)/(8)} \\ s=\sqrt[]{((-4.77)^2+(13.83)^2+(2.83)^2+(-11.97)^2+(-7.17)^2+(3.83)^2+(16.53)^2+(-14.77)^2+(1.63)^2)/(8)} \\ s=\sqrt[]{(22.72+191.36+8.03+143.2+51.36+14.69+273.35+218.05+2.67)/(8)} \\ s=\sqrt[]{(925.44)/(8)} \\ s=\sqrt[]{115.68} \\ s=10.76 \end{gathered}$

Therefore, the sample standard deviation of the given dataset rounded to two decimal places is 10.76.

Variance

The standard deviation is the square root of the variance. Thus, the formula to find the variance of a sample is,

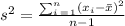
$s^2=\frac{\sum^n_{i\mathop{=}1}(x_i-\bar{x})^2}{n-1}$

So, in this case, we have:

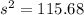
Therefore, the sample variance of the given dataset rounded to two decimal places is 115.68.

Population

Standard deviation

The population standard deviation formula is:

$\begin{gathered} \sigma=\sqrt[]{\frac{\sum ^n_{i\mathop{=}1}(x_i-\bar{x})^2}{N}} \\ \text{Where} \\ \sigma\text{ is the population standard deviation} \\ x_i\text{ is each of the values of the data} \\ N\text{ is the number of data points} \end{gathered}$

So, in this case, we have:

$\begin{gathered} s=\sqrt[]{((23.5-28.27)^2+(42.1-28.27)^2+(31.1-28.27)^2+(16.13-28.27)^2+(21.1-28.27)^2+(32.1-28.27)^2+(44.8-28.27)^2+(13.5-28.27)^2+(29.9-28.27)^2)/(9)} \\ s=\sqrt[]{((-4.77)^2+(13.83)^2+(2.83)^2+(-11.97)^2+(-7.17)^2+(3.83)^2+(16.53)^2+(-14.77)^2+(1.63)^2)/(9)} \\ s=\sqrt[]{(22.72+191.36+8.03+143.2+51.36+14.69+273.35+218.05+2.67)/(9)} \\ s=\sqrt[]{(925.44)/(9)} \\ s=\sqrt[]{102.83} \\ s=10.14 \end{gathered}$

Therefore, the population standard deviation of the given dataset rounded to two decimal places is 10.14.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Mean

Standard deviation

Variance

Standard deviation

0 Comments

Please log in or register to add a comment.

Other Questions