Answer:
All the options are correct
Explanations:
A quick and smart way is to substitute a value for x in each of the options and verify if the right hand side equals the left hand side
Let x = 30
A) (sin x + cos x)² = 1 + sin 2x
(sin 30 + cos 30)² = 1.866
1 + sin 2(30) = 1.866
Therefore (sin x + cos x)² = 1 + sin 2x
B)
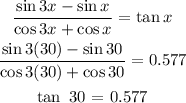
Therefore:
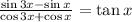
C) sin 6x = 2 sin3x cos3x
sin 6(30) = 0
2 sin3(30) cos3(30) = 0
Therefore sin 6x = 2 sin3x cos3x
This can also be justified by sin2A = 2sinAcosA
D.
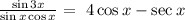
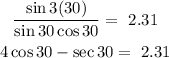
Options A to D are correct