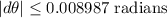Given: A surveyor standing 50 feet from the base of a large tree measures the angle of elevation to the top of the tree as 75.8 degrees.
Required: To determine how accurately the angle must be measured if the percent error in estimating the tree's height is less than 5%.
Explanation: To estimate the angle, we will use the trigonometric ratio
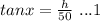
where h is the tree's height, and x is the angle of elevation to the top of the tree.
Hence we get
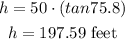
Now differentiating equation 1, we get
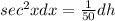
We can write the above equation as:
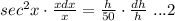
Also, it is given that the error in estimating the tree's height is less than 5%.
So
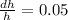
Also, we need to convert the angle x in radians:
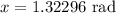
Putting these values in equation (2) gives:

Solving the above equation gives:
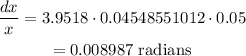
Let
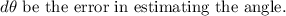
Then,
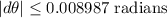
Final Answer: