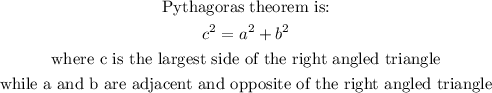In order to know if 3 squares will form a right triangle,
a. The sum of the length of two of the squares must be greater than the length of the last square.
b. The lengths of the squares (if they are integers) must form a Pythagorean triple.
Pythagorean triples are:
3, 4, 5
5, 12, 13
8, 15, 17
9, 40, 41
there are more triples but we only need these for this question
c. They must conform to the Pythagoras Theorem.

Now we can proceed with these points at hand.
1. Squares with side lengths 6, 8, 10 can be written as:
2(3), 2(4), 2(5).
Ignoring the "2", we can see that this follows the Pythagorean triple.
therefore, 6, 8, 10 can form a right-angled triangle
2. 64, 100, 144 can be written as:
4(16), 4(25), 4(36)
Ignoring the "4", we can see that this does not follow the Pythagorean triple.
If we input the values into the Pythagoras theorem, we shall have:
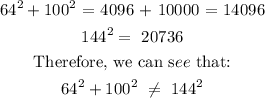
Therefore, 64, 100, 144 cannot form a right-angled triangle
3. Two squares with lengths 5 and a Square with an area of 50 square feet:
We need to find the length of the square with an area of 50 square feet.
![\begin{gathered} \text{Area of square = l}^2 \\ \text{where l is the length of the side} \\ 50=l^2 \\ \text{square root both sides} \\ l\text{ = }\sqrt[]{50\text{ }}\text{ = 5}\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9xmzd6d767it6mjbdyamnsmn5c2jskazd7.png)
Now that we know the length of the 3rd and largest side of this triangle, we can now determine whether it is a right-angled triangle.
This case has a non-integer as part of the sides of the triangle, thus, condition b does not apply.
We must check via Pythagoras theorem:
![\begin{gathered} By\text{ pythagoras:} \\ 5^2+5^2=25+25=50 \\ \text{while,} \\ (5\sqrt[]{2})^2=5^2*(\sqrt[]{2})^2=25*2=50 \\ \text{Thus we can s}ee\text{ that:} \\ 5,5,5\sqrt[]{2}\text{ can form a right-angled triangle} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9rm5pn9ljapd1o22k8mphngznhxiq45z7d.png)
Therefore, the final answer: 1 and 3 can form a right-angled triangle but 2 cannot
4. I have given the reasons why they form a right-angled triangle above. But let me restate them:
In order to know if 3 squares will form a right triangle,
a. The sum of the length of two of the squares must be greater than the length of the last square.
b. The lengths of the squares (if they are integers) must form a Pythagorean triple.
Pythagorean triples are:
3, 4, 5
5, 12, 13
8, 15, 17
9, 40, 41
there are more triples but we only need these for this question
c. They must conform to the Pythagoras Theorem.